Los árboles en Estructura de Datos.-

Un árbol es una estructura de datos ampliamente usada que imita la forma de un árbol (un conjunto de nodos conectados). 

Estos nodos son las unidades sobre la que se construye el árbol y puede tener cero o más nodos hijos conectados a él. 

Se dice que un nodo  es padre de un nodo  si existe un enlace desde  hasta  (en ese caso, también decimos que  es hijo de ). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos se conoce como hoja. Los demás nodos (tienen padre y uno o varios hijos) se les conoce como rama.

Uso de los árboles.-

• Representación de datos en jerarquía.
• Como ayuda para realizar búsquedas en conjuntos de datos.

Formalmente, podemos definir un árbol de la siguiente forma:

• Caso base: un árbol con sólo un nodo (es a la vez raíz del árbol y hoja).

• Un nuevo árbol a partir de un nodo 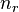 y  árboles  de raíces  con  elementos cada uno, puede construirse estableciendo una relación padre-hijo entre 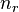 y cada una de las raíces de los  árboles. 

Una sucesión de nodos del árbol, de forma que entre cada dos nodos consecutivos de la sucesión haya una relación de parentesco, decimos que es un recorrido árbol. Existen dos recorridos típicos para listar los nodos de un árbol: primero en profundidad y primero en anchura. En el primer caso, se listan los nodos expandiendo el hijo actual de cada nodo hasta llegar a una hoja, donde se vuelve al nodo anterior probando por el siguiente hijo y así sucesivamente. En el segundo, por su parte, antes de listar los nodos de nivel  (a distancia  aristas de la raíz), se deben haber listado todos los de nivel . Otros recorridos típicos del árbol son preorden, postorden e inorden:

• El recorrido en preorden, también llamado orden previo consiste en recorrer en primer lugar la raíz y luego cada uno de los hijos  en orden previo.
• El recorrido en inorden, también llamado orden simétrico (aunque este nombre sólo cobra significado en los árboles binarios) consiste en recorrer en primer lugar , luego la raíz y luego cada uno de los hijos  en orden simétrico.
• El recorrido en postorden, también llamado orden posterior consiste en recorrer en primer lugar cada uno de los hijos  en orden posterior y por último la raíz.

Operaciones básicas con árboles.-

Las operaciones comunes en árboles son:

• Enumerar todos los elementos.
• Buscar un elemento.
• Dado un nodo, listar los hijos (si los hay).
• Borrar un elemento.
• Eliminar un subárbol (algunas veces llamada podar).
• Añadir un subárbol (algunas veces llamada injertar).
• Encontrar la raíz de cualquier nodo.

Por su parte, la representación puede realizarse de diferentes formas. Las más utilizadas son:

• Representar cada nodo como una variable en el heap, con punteros a sus hijos y a su padre.
• Representar el árbol con un array donde cada elemento es un nodo y las relaciones padre-hijo vienen dadas por la posición del nodo en el array.

Clasificación de árboles.-

Árbol Binario.-

En ciencias de la computación, un árbol binario es una estructura de datos en la cual cada nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda, los montículos binarios y Codificación de Huffman. 

Un árbol ordenado es aquel en el que las ramas  de los nodos del árbol están  ordenadas. Los árboles ordenados de grado 2 son de especial interés puesto que  representan una de las estructuras de  datos más importantes en computación, conocidas como  árboles binarios. En un árbol binario cada nodo puede tener como máximo dos subárboles y  siempre es necesario distinguir entre el subárbol izquierdo y el subárbol derecho.

Formalmente podemos definir un árbol binario de tipo T como una estructura homogénea que es la concatenación de un elemento de tipo T, llamada raíz, con dos árboles binarios disjuntos. Una forma  particular de árbol binario puede ser la estructura vacía. 

Los árboles binarios  se clasifican en cuatro tipo que son : distintos, similares, equivalentes y completos. Cuando dos  árboles binarios se dice que son similares si tiene la misma estructura y son equivalentes  si son similares  y contienen la misma información. En caso contrario  se dice que  estos árboles son distintos. Un arbol binario esta equilibrado  si la altura de los dos subárboles  de cada nodo del arbol  se diferencia en una unidad como máximo. 

El procedimiento de arbol binarios equilibrados es mas sencillo que los árboles no equilibrados.